Approximating pi with lego

Overview

With lego I've made a slider-crank linkage, which moves in an approximation of cosine. I attached a digital caliper to measure the movement of the rod.

With these measurements I can create a 400-sided polygon (like an octogon but 50 times better) that can be broken into 400 triangles. The total area of these triangles approximates that of a circle. I finally took the formula for the area of a circle and solved for pi.

I got 3.1377, an error of 0.12%.

(If I instead use the data to adjust cosine--see below--I get 3.1414, an error of 0.005%.)

What went wrong

• I could not get a lot of data points because I had to read the data myself from the caliper. With some OCR, I could have left the thing to run for an hour and get thousands of measurements.
• Due to my lack of lego pieces, the length of the shaft was limited. With a longer shaft, the crank could have been bigger without sacrificing accuracy. Bigger crank == more movement == easier to measure.
• The whole thing is made of legos and held up by rubber bands. It bends and fudges measurements.

What it looks like

Setup

Caliper and crank

Motor

Movement

Hardware

• A variety of lego technic pieces
• An old model of the Adafruit Arduino motor shield
• An Arduino Uno
• A 200-step 12V stepper motor (in interleaved mode it actually does 400 steps at half torque, source)
• A cheap digital caliper
• Some various-sized bolts to secure the motor to the lego
• Some rubber bands to secure the caliper to the lego

Data collection

Connecting to the Arduino to control the motor

The pyserial library makes it pretty easy to send commands to your Arduino. On the Arduino side, you can see an example in the IDE at File > Examples > 04. Communication > ReadASCIIString.

import serial

# On linux you can run `dmesg | grep tty` to find your Arduino
ser = serial.Serial('/dev/ttyACM0', 115200, timeout=1)

# Assuming your Arduino accepts numbers as commands,
# Move it forward 10 steps
ser.write(f"10\n".encode())

# Move it backwards 5 steps
ser.write(f"-5\n".encode())

Capturing an image of the caliper LCD

OpenCV is great for getting images from your webcam. I pointed the webcam to the caliper's LCD screen and took images inbetween movements of the motor.

I couldn't get tesseract to work recognizing the 7-segment display of my caliper, so I just read the values by hand.

import numpy as np
import cv2 as cv
from datetime import datetime

# With `num` being the position/angle of the motor, take a photo of the caliper
# to get the position of the crank
def capture_cam(num):
    # Read from device 0, by default
    cap = cv.VideoCapture(0)

    if not cap.isOpened():
        print("Cannot open camera")
        exit()

    ret, frame = cap.read()
    cap.release()

    # crop
    frame = frame[120:120+225, 150:150+400]

    # Write the image to a file for a human to read
    cv.imwrite(f"./{num}_{datetime.now().time().strftime('%H%M%S')}.jpg", frame)

This is what an image looks like. Fairly easy for a human to capture.

However, do NOT walk away and turn off the lights. You'll have to squint a lot more.

Getting everything together

Raw data

I save the data (by hand) into a Python list. This list is 400-long, which is the number of steps in a full revolution of the stepper motor.

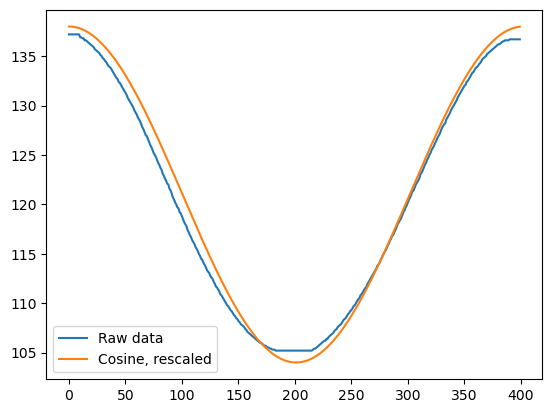
Here is what this data looks like. By trial-and-error I've overlaid the real cosine as best as I could. You can see that the raw data is flatter than the real thing: this is because the crank loses torque at the extreme ends and so becomes less responsive.

This Wikipedia page gives a good explanation of the mechanics of the slider crank: https://en.wikipedia.org/wiki/Slider-crank_linkage It's important to consider that the mechanism is more accurate the smaller the crank is relative to the shaft; however, the smaller the crank, the less movement, so your caliper may not keep up!

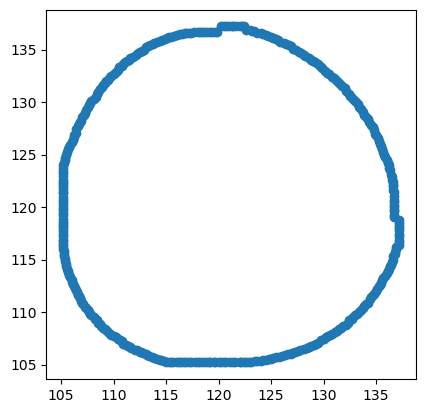
Our beautiful circle

To draw a circle you need sine and cosine. We have cosine (x), so to get sine (y) we just need to shift our data by 1/4 of a full revolution, 100 steps.

With x and y we can make a circle! The odd shape of the circle is due to the limitations of the physical setup. :-(

Calculating the area of our circle

Our series of points approximate a circle, but really what they are is a 400-side polygon. Still, it looks close enough if you look at it from the other room.

We can calculate the area of our 400-sided polygon by breaking it down into 400 triangles. The area of the whole thing will be close to that of a similar-sized circle.

# Given our series of points for x and y,
# The center/centroid of the shape is
cx = sum(x)/len(x)
cy = sum(y)/len(y)

# Given three points of a triangle, with one point always being the center,
# the area of the triangle is
def triangle_area(ax, ay, bx, by, cx, cy):
    return abs(ax*(by-cy)+bx*(cy-ay)+cx*(ay-by))/2

total_area = 0

# Calculate the area of each triangle
# a is the first point, b the next point, and c the center point (constant)
for i in range(len(x)):
    ax = x[i]
    ay = y[i]
    bx = x[(i+1) % len(x)]
    by = y[(i+1) % len(y)]
    print(triangle_area(ax, ay, bx, by, cx, cy))
    total_area += triangle_area(ax, ay, bx, by, cx, cy)

print(total_area)

Calculating pi

We can then approximate pi by getting the radius of our circle then using that with the area to solve for pi.

radius_sum = 0

# Calculate the radius as the average distance between each point and the centroid
for i in range(len(x)):
    ax = x[i]
    ay = y[i]
    radius_sum += math.sqrt((cx-ax)**2 + (cy-ay)**2)

radius = radius_sum/len(x)
print(radius)

Pi is then approximately

print(total_area / radius**2,
  ", true pi: ", math.pi,
  ", error: ", f"{((total_area / radius**2) - math.pi)/math.pi:%}")

3.1376680564858788 , true pi:  3.141592653589793 , error:  -0.124924%

What if?

Above I overlaid the raw data with cosine. What if this series were used instead?

data = [17*math.cos((x-0)/64)+121 for x in range(400)]
x = data
y = [data[(i+100) % len(data)] for i in range(len(data))]

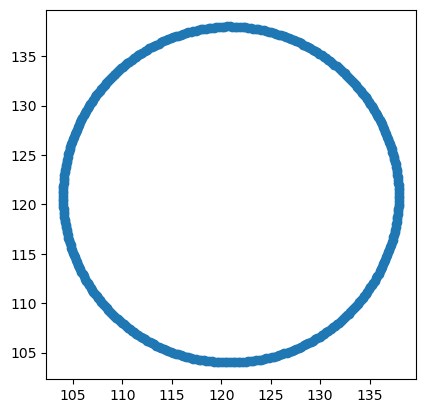
If we then approximate pi from this data, we get a better result.

3.1414322671587436 , true pi:  3.141592653589793 , error:  -0.005105%